TP 2: segmentation and classification of PreTest signals¶

Balthazar Neveu

Topics:

  • Noisy labels
  • Imbalanced dataset
  • Feature extraction
  • Dimension reduction

Problem statement¶

  • Total normal samples: 85 = 35.1%
  • Total tight samples: 157 = 64.9% (dominant class)

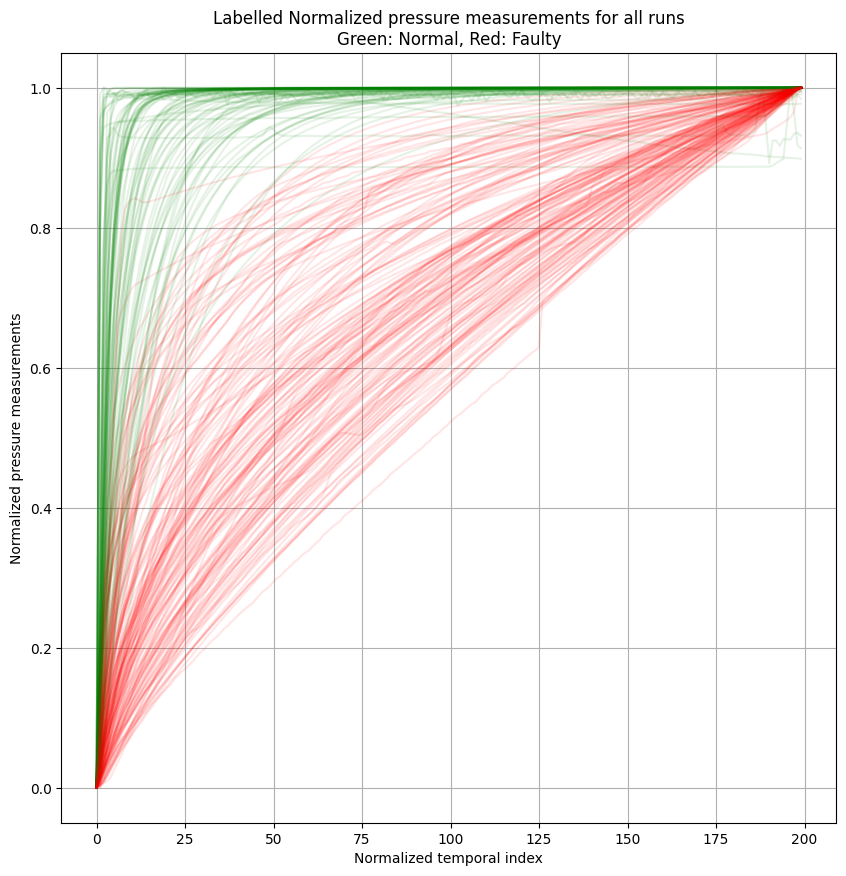
profiles classification

  • Classify a set of pressure profiles.
    • 🟢 Green: normal $\text{label}=1$
    • 🔴 Red: Tight $\text{label}=0$

Exploration: Reparameterization and handcrafted features¶

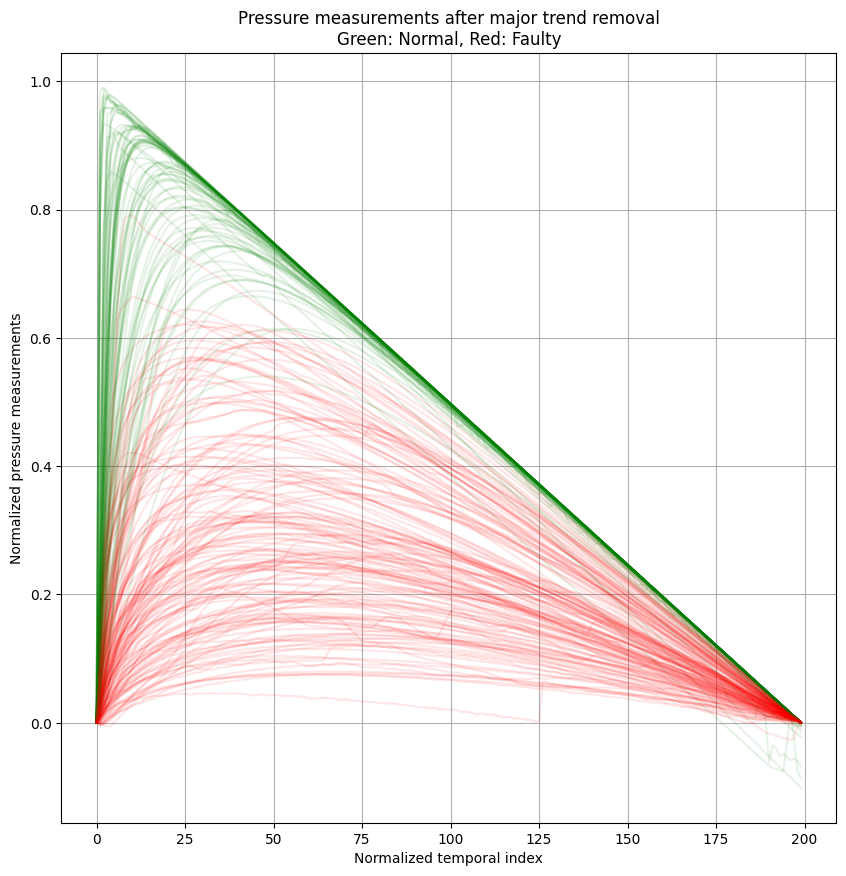
profiles classification minus trend

  • Remove the "identity trend"
  • Maximum value of these curves looks like a good discriminator.

Exploration: Handcrafted feature¶

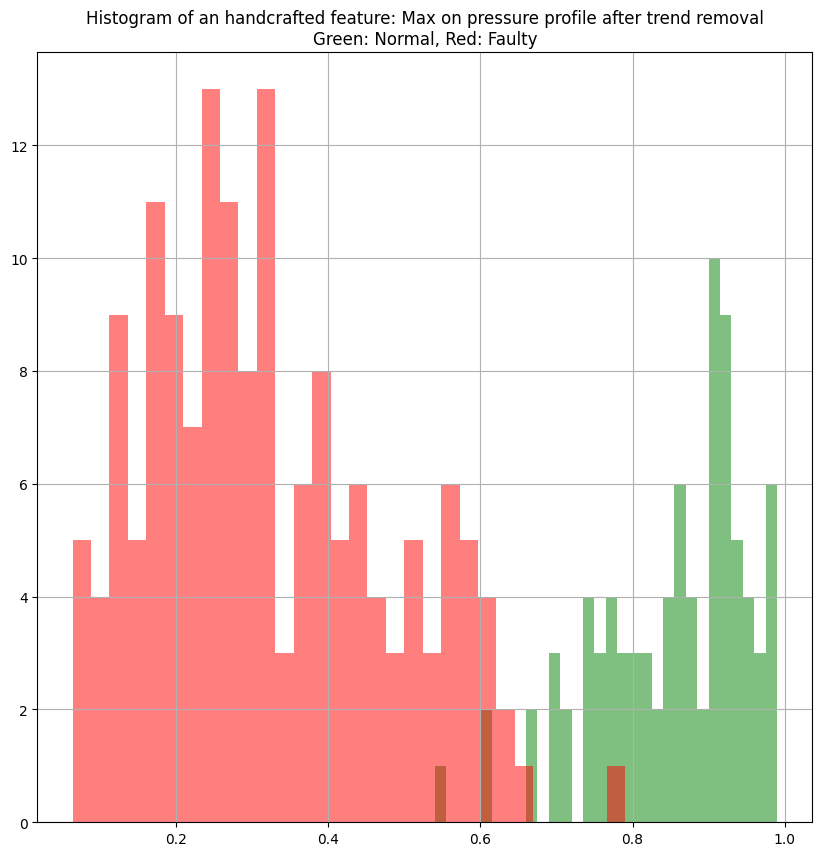
profiles classification

  • Histogram of this handcrafted feature for the 2 labelled classes.
  • A simple threshold around 0.7 could be enough to discriminate these 2 classes. Simple to compute, yet seems efficient.

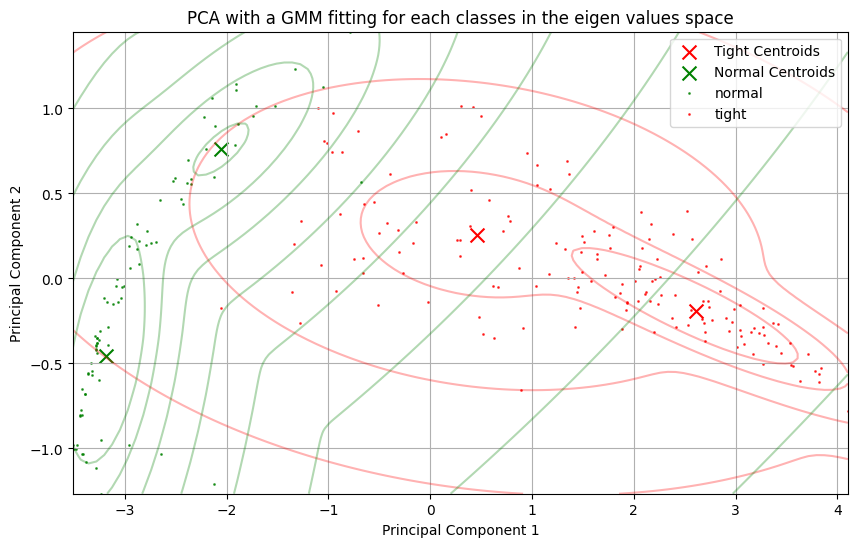
Exploration: PCA¶

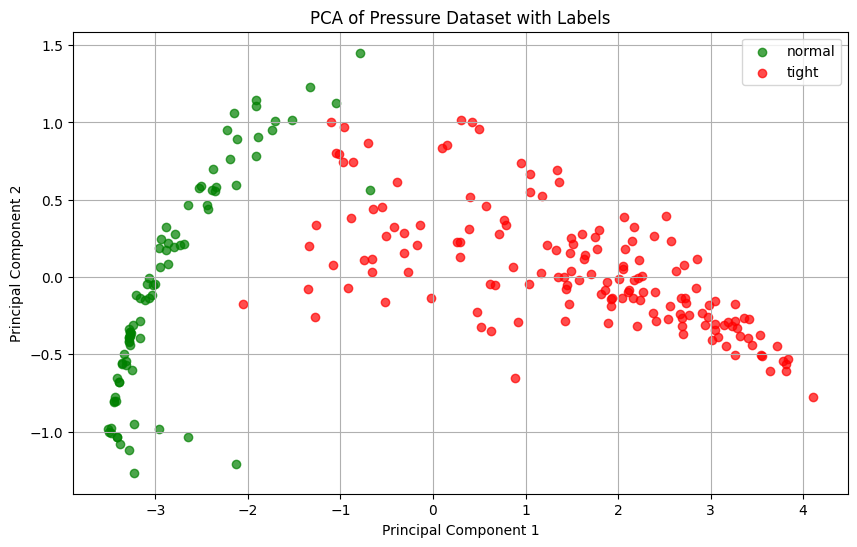
  • When we apply a principal component analyzis to the raw curves, we're able to see 2 clusters appear in the 2D eigen cofficient space.
  • Each pressure curve made of 200 samples has been mapped to a single 2D vector.
  • Knowing the labels, 2 obvious clusters appear.

pca

2D Gaussian Fitting¶

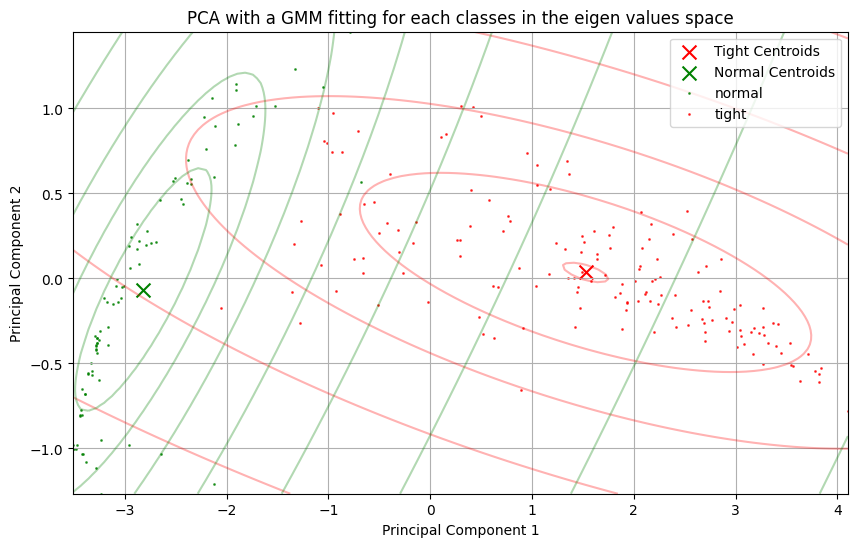
gaussian fit

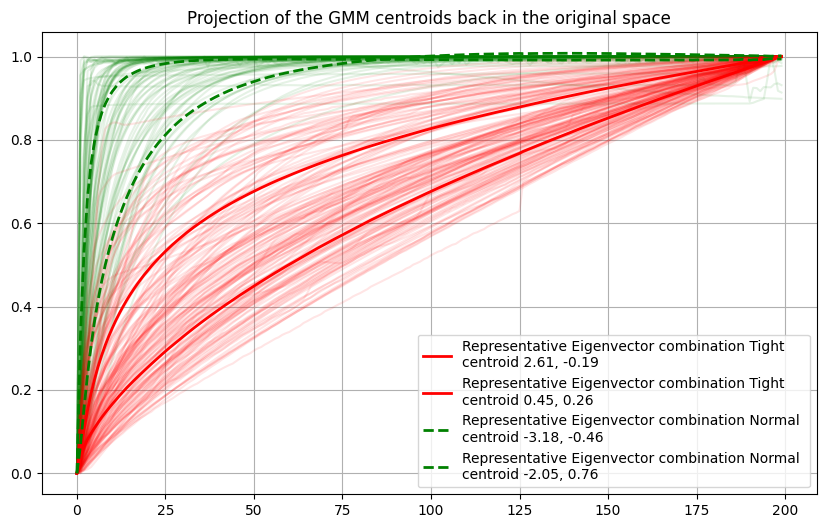
  • If we reproject the centroid back into the original pressure curve space, we can see that these curves are pretty representative of the 2 distributions in the original space.
  • These are simple combinations of the 2 eigenvectors.

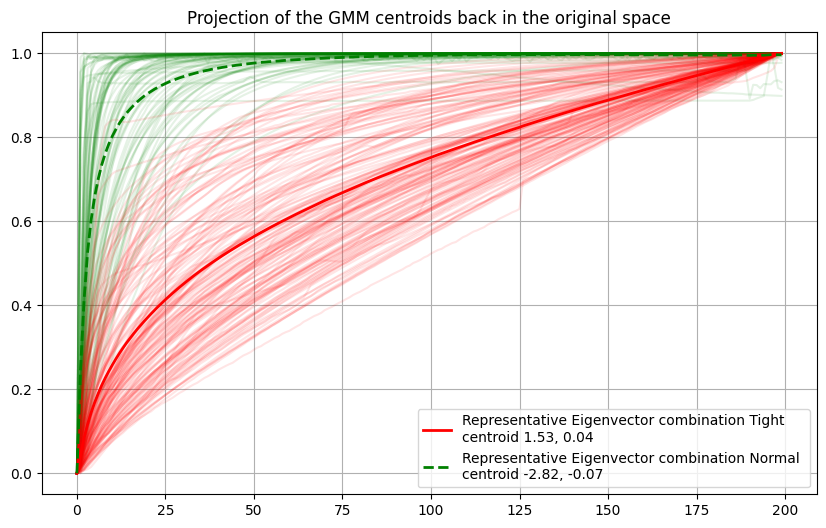
gaussian fit reproj

Please note that scikitlearn applies a mean centering to perform PCA

Fitting a 2D GMM (Gaussian Mixture Model)¶

gaussian fit 2 modes

gaussian fit 2 modes reproj

Classification¶

  • Precision: classified a normal event as normal $\frac{tp}{tp+fp}$: classifier ability not to label as positive a sample that is negative. 💲
  • Recall: classified $\frac{tp}{tp+fn}$ : the classifier ability to find all the positive samples.. We want a recall of 100% here ❌ !
  • Confusion matrix: $C_{i, j}$
    • $i$ groundtruth class
    • $j$ predicted class
Confusion matrix Prediction $j=0$ Tight Prediction $j=1$ Normal
Groundtruth $i=0$ Tight True Negative (groundtruth=tight, prediction=tight) ✔️ False Positive (groundtruth=tight,prediction=normal) 💲
Groundtruth $i=1$ Normal False Negative (groundtruth=normal, prediction=Tight) ❌ True Positive (groundtruth=normal, prediction=normal) ✔️

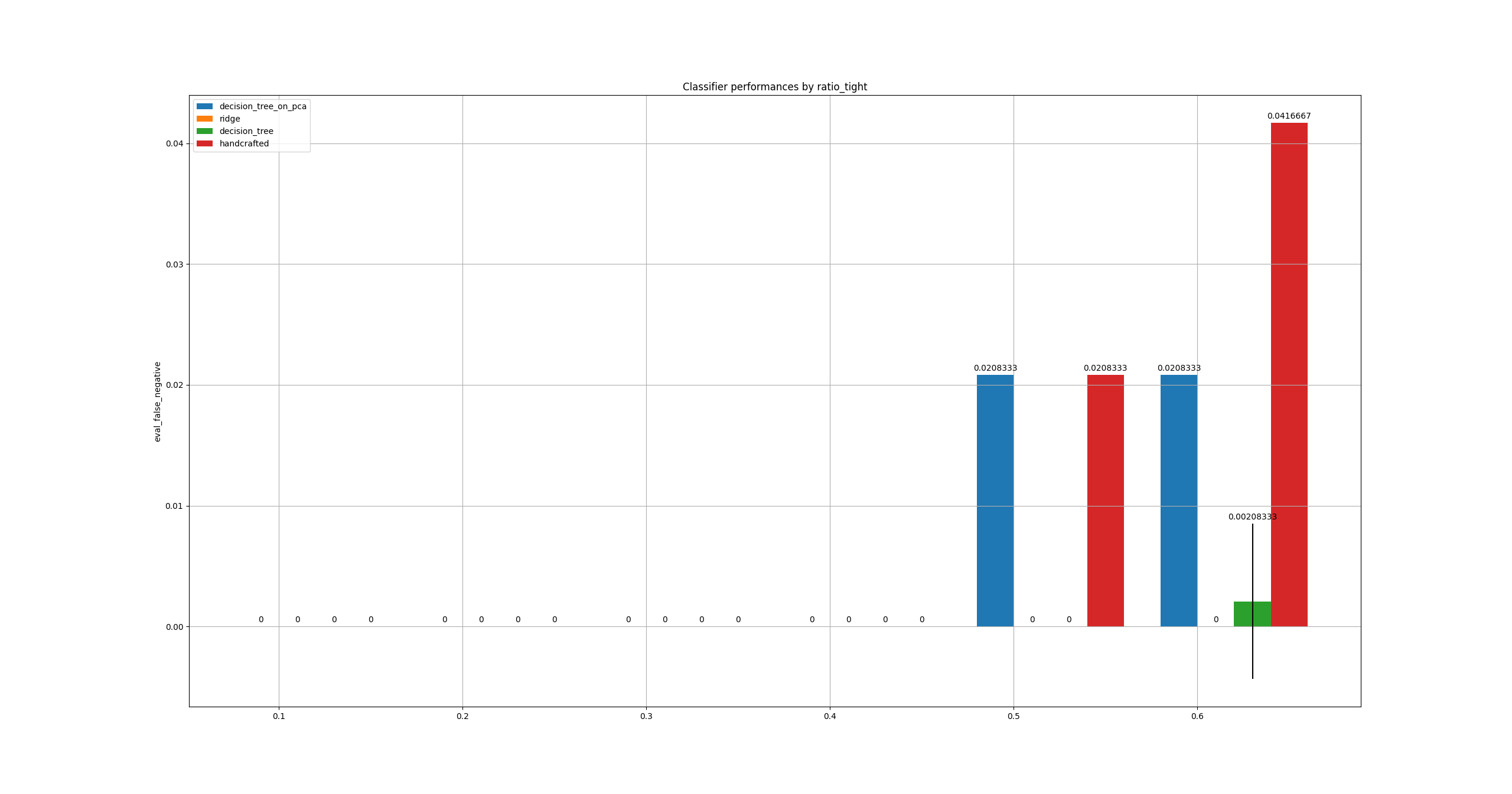
Study with regard to pressure test length¶

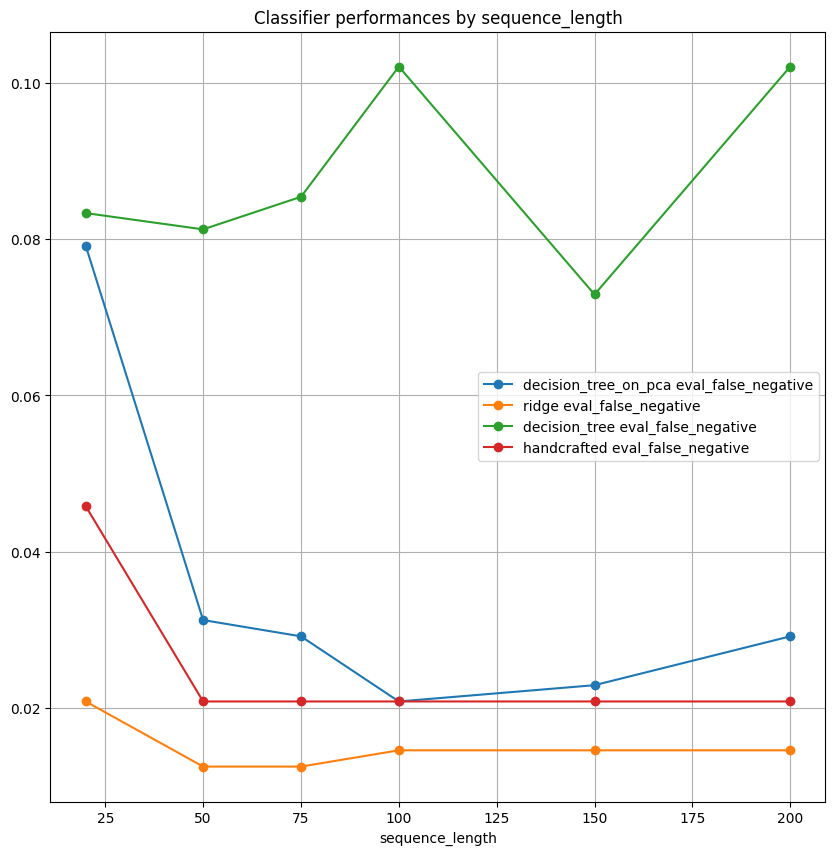
Study with regard to labelling quality¶

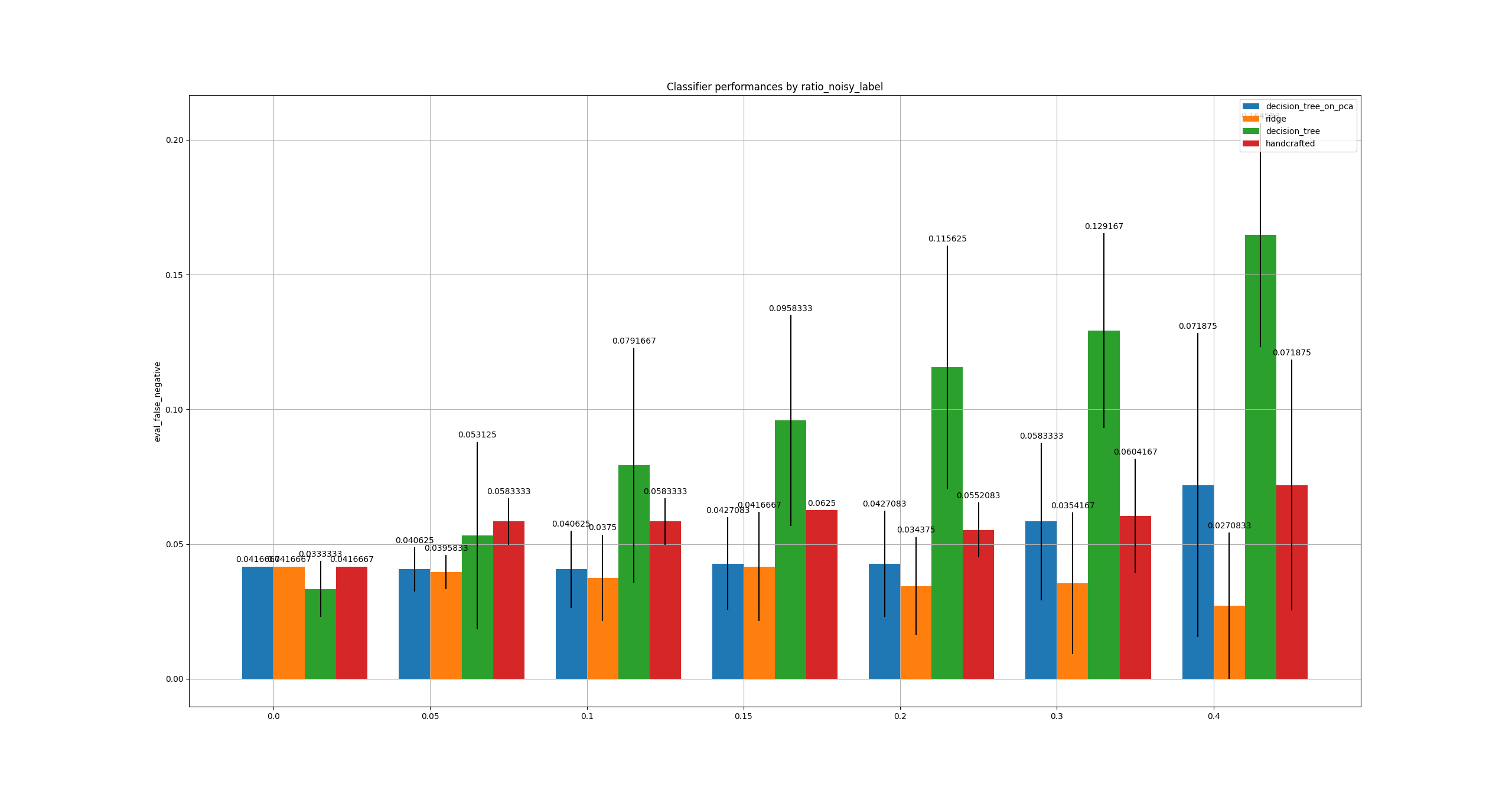
Study with regard to dataset imbalance¶

  • Does not seem very sensitive.

Conclusions¶

  • Very low data regime.
  • Simplicity: Handcrafted features with very basic classifier achieves quite decent results.
  • False Negative is the most important metric for this topic. False Positives may increase costs.
  • More work to be done to decrease and reach 0% of false positives, either by adding metadata or making more complex classifiers.
  • Class imbalance does not seem to affect results too much here. Noisy labels either.
  • Known method limitations:
    • Cross validation is performed by sampling several noisy train sets... while test set remains the same to get a fixed test set reference without noise.
    • Not using metatada
    • No true way to specifically minimize false negatives.
    • Quid: resampling on time dimension, did we loose information

How to use?¶

  • Notebook
  • Command line interface:
    • python TP_2/code/train_classifiers.py --study sequence_lengths_study_noisy -r 20
    • Choices of studies:
      • sequence_lengths_study: vary pressure test duration, perfect labels, perfect class balance (50%-50%)
      • sequence_lengths_study_noisy: vary pressure test duration, slightly noisy labels (20%)
      • noisy_labels_study: study the influence of the amount of noisy labels on final performances.
      • tight_ratio: tight class ration: variation of class imbalance